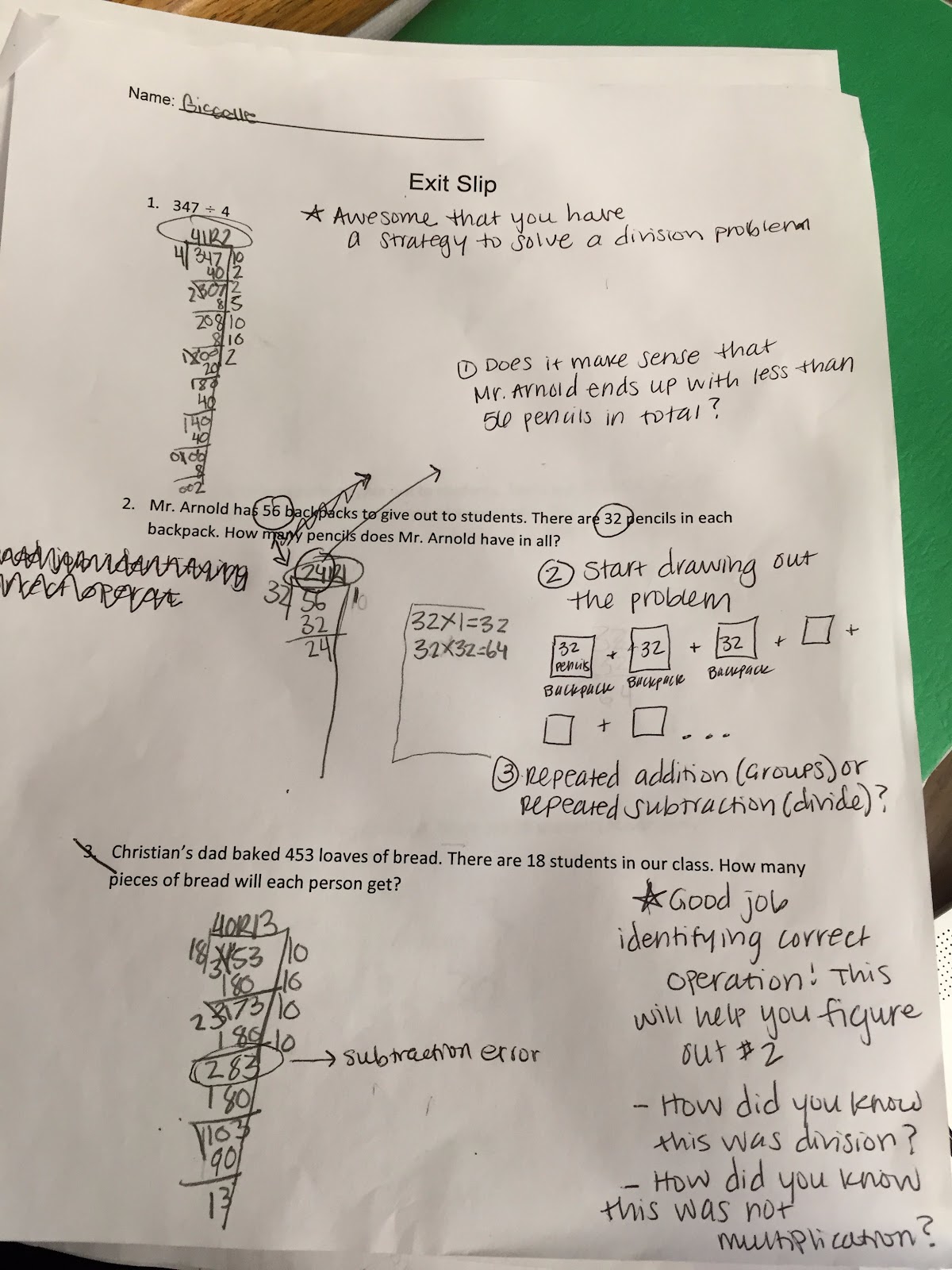
In math we are working on identifying correct operations in multiplication and division word problems as well as finding strategies that we are comfortable with to solve multiplication and division problems. The purpose of this exit ticket was to identify if students were able to find a strategy they were comfortable with to correctly solve a division problem (number 1), see whether students could interpret the difference between a division and multiplication word problem (numbers 2 and 3) and assess whether they could choose a strategy to solve the division or multiplication word problem (numbers 2 and 3). The two learning objectives posted for this lesson were:
The feedback provided to Gisselle provided her strengths and areas for improvements based on the two learning objectives. I identified her strength in question number 3 as being able to identify the correct operation. This tells me that once she sees a division problem, she is able to utilize a strategy. This strength, I noted would help her with her weakness in number two of incorrectly identifying the operation (LO 1). The leading questions on the exit ticket are provided to encourage her to think about how she thought about the problem. If she was successful in identifying the operation in this particular question then getting her to think about how she knew it was a division problem will aid her in understanding that number 2 is a multiplication problem and not division.
An area for improvement for Giselle is identifying multiplication problems within word problems (LO 1) and finding a strategy she is comfortable with to solve the multiplication word problem (LO2). A part of understanding whether it is a multiplication or division problem is figuring out whether the final answer makes sense in the context of the story. Therefore, I wrote “Does it make sense that Mr. Arnold puts 32 pencils in 56 backpacks and then ends up with less pencils than would be in one backpack?” in order for her to see it would not make sense for there to be 24 pencils in total. Then, I encourage her to start drawing out what the problem is asking her to do. I want her to use her strength from number 3 of identifying the division problem correctly to inform how she is going to draw out the problem. I give her a start by drawing a backpack and putting 32 pencils in there and have her finish the rest. Then my next leading question asks what she is doing. Is it repeated addition or repeated subtraction? My hope is that hint will give her an idea that when she is adding groups of something over and over again, an efficient strategy to use is multiplication (LO2). I would then monitor her thinking to understand what strategy she uses for multiplication (box method is a strategy that our 5th graders should be proficient in) to inform next steps with multiplication strategies.
While it was not an explicit focus of the two learning objectives but rather a byproduct of using the Big 7 strategy or division in general, I will create another differentiated grouping based on students who need support with subtraction. My feedback on the exit tickets were not tailored toward this but it is important to note that Gisselle struggled with subtraction. In order to give her additional support, I will start incorporating math routines, creating number lines, and drawing pictures. This will serve as a basis and bridge to doing a standard algorithm approach with borrowing. An example of a math routine that could target subtraction skills is count around the circle as stated in “Number Sense Routines” by Jessica Shumway. In this routine, students count backwards by a certain constant number in a circle while I make it visual on the board.
Learning objective 1: I can interpret division and multiplication word problems to identify the correct operation.
Learning objective 2: I can use a strategy I am comfortable with to solve multiplication and division word problems.
Feedback-Gisselle
The feedback provided to Gisselle provided her strengths and areas for improvements based on the two learning objectives. I identified her strength in question number 3 as being able to identify the correct operation. This tells me that once she sees a division problem, she is able to utilize a strategy. This strength, I noted would help her with her weakness in number two of incorrectly identifying the operation (LO 1). The leading questions on the exit ticket are provided to encourage her to think about how she thought about the problem. If she was successful in identifying the operation in this particular question then getting her to think about how she knew it was a division problem will aid her in understanding that number 2 is a multiplication problem and not division.
An area for improvement for Giselle is identifying multiplication problems within word problems (LO 1) and finding a strategy she is comfortable with to solve the multiplication word problem (LO2). A part of understanding whether it is a multiplication or division problem is figuring out whether the final answer makes sense in the context of the story. Therefore, I wrote “Does it make sense that Mr. Arnold puts 32 pencils in 56 backpacks and then ends up with less pencils than would be in one backpack?” in order for her to see it would not make sense for there to be 24 pencils in total. Then, I encourage her to start drawing out what the problem is asking her to do. I want her to use her strength from number 3 of identifying the division problem correctly to inform how she is going to draw out the problem. I give her a start by drawing a backpack and putting 32 pencils in there and have her finish the rest. Then my next leading question asks what she is doing. Is it repeated addition or repeated subtraction? My hope is that hint will give her an idea that when she is adding groups of something over and over again, an efficient strategy to use is multiplication (LO2). I would then monitor her thinking to understand what strategy she uses for multiplication (box method is a strategy that our 5th graders should be proficient in) to inform next steps with multiplication strategies.
**Note, I also noticed she was unable to subtract correctly. In order to not make the feedback overwhelming for her on this exit ticket, I focused my attention on the two learning objectives but am using what I notice about her subtraction skills to inform math activity routines and potential interventions in the next steps section.
Feedback-Shirley
The feedback provided to Shirley shows mastery of one of the learning objectives which will aid her in mastering the other learning objectives. The strength was that she was able to pick out a strategy she was comfortable with to solve a division problem (number 1; LO 2). She successfully used the “Big 7” strategy with accurate subtraction computation. This strength, I noted, will help her in solving the word problems below.
I identified Shirley’s weakness on the first learning objective. She was unable to interpret word problems to understand which operation she needed to use. The first piece of feedback I provided was to ask if the answer makes sense. So, does it make sense that each student will get more bread than is actually available? That should give her a hint that her answer is unrealistic. I did the same thing for the other word problem. “Does it make sense that Mr. Arnold has one pencil after starting out with 32 in one backpack?” This should get her thinking about how realistic her answer is. The next piece of advice I gave is to draw it out. I started her off in number 2 by drawing the backpacks and pencils in each backpack. The leading question for both number 2 and 3 of “is this repeated addition or repeated subtraction? What operation would you use for either of those” and “are you making groups of things or are you dividing things out” will encourage her to think about the problem within context to aid in understanding what operation to use.
It was interesting to note that Shirley’s strength of knowing how to use a division strategy and weaknesses of doing the incorrect operations might indicate that she has trouble with reading comprehension and/or language. This is something that I noticed in reading as well so there are cross-applications between subjects as well. 
Next Steps
Based on the strengths and areas for growth, I will create skill based groupings in our differentiated math rotations. The group that will be applicable to both Shirely and Gisselle will focus on identifying correct operations in word problems. This is based on both Shirely and Gisselle needing additional support in interpreting word problems shown from the exit ticket. They both had a strategy to solve a multiplication or division problem but did not have the comprehension of the word problem to understand which operation to use. This will also extend the learning on the feedback I provided them on their papers. In this group I will begin with manipulatives and tangible word problems that are easy for students to interpret. For example, I will start with a 2X1 division problem that has to do with dividing out blocks between friends. I will use blocks or cubes to demonstrate my thinking about the problem and have them do the same. This way it is tangible, hands on, and tied to context. I will do a similar strategy for multiplication. Once we have mastered the strategy with manipulatives, I will have them try by drawing it out on paper. Each time they find themselves starting to group things and add them, it will be a hint that it is a multiplication problem. Each time they find themselves dividing things out and repeatedly subtracting, it will be a hint that it is subtraction. After they have successfully used manipulatives and the drawing out strategy to interpret what the problem is asking them to do, I will hand out two student exit tickets and ask them to identify the misconception. One student copy will correctly identify the operation and one student copy will incorrectly identify the operation. Leading questions that will be asked:
1. “Does the final answer realistically make sense?”
2. Draw it out--
a.“Are you creating groups of things and adding them?”
b.“Are you dividing things out between people?”
3. “What strategy would be the most efficient to use depending on if you are doing a or b?
They will have to justify their thinking. Through talking it out, I will be able to understand what students are thinking when they identify the correct operation and they will be forced to justify their thinking through a more inquiry based process that is more meaningful to them. Last, I will have them use the strategies we practiced above to revise their exit tickets.
While it was not an explicit focus of the two learning objectives but rather a byproduct of using the Big 7 strategy or division in general, I will create another differentiated grouping based on students who need support with subtraction. My feedback on the exit tickets were not tailored toward this but it is important to note that Gisselle struggled with subtraction. In order to give her additional support, I will start incorporating math routines, creating number lines, and drawing pictures. This will serve as a basis and bridge to doing a standard algorithm approach with borrowing. An example of a math routine that could target subtraction skills is count around the circle as stated in “Number Sense Routines” by Jessica Shumway. In this routine, students count backwards by a certain constant number in a circle while I make it visual on the board.
A couple of thoughts: First, your feedback is very clearly written and includes both a strength and an area of growth for each student. Your suggestion for Giselle to start drawing out the problem is very useful. Leave out the + signs between the pictures though--putting them there means she doesn't really have to think about whether it's repeated addition or repeated subtraction--feedback you gave that does help her with LT1. Let her do the thinking on that part!
ReplyDeleteWhat I see in both Shirley and Giselle's work is evidence that the algorithms are not meaningful operations for them, even though they can (mostly) successfully use the algorithms to solve problems. I don't think it's just that they don't understand the story or that they don't know what operation to use, I think it's that all these different aspects of problem solving in math are very disconnected for them. They see the Big 7 algorithm as a way to solve a problem like 347 / 4, rather than as a way to find out how many 4s are in 347. This is an important difference, and the essence of your learning target 1. Notice that Shirley started #3 by drawing out 18 circles. My guess is she could have solved this problem if she had modeled it completely, but the large number made her turn to an algorithm. My guess is that she thought that it would be "a lot of bread" for each person, and so chose multiplication because she associates multiplication with making bigger (and each person was going to get a lot of bread=big number=multiplication). Your redirection/feedback to both to draw pictures and to think about what the answer should be is right on for what they need. And your plan to do more number sense routines is also a good idea. I think you also want to do some more intentional work around making sense of what each algorithm is finding. Like big 7 is helping you find out how many 4s are in 347. Sometimes we only ask students to make sense of their answer like this with problems in context--do the exact same work with the algorithms. Ask them to explain why their answer makes sense for the algorithms too.
Let's talk about this some more in person!